byjusfutureschool

Gratis un mes de programación en Byjus Future School.

Llena el formulario que esta debajo del vídeo para que agendes un mes gratis de programación para los mas pequeños.

 

Matriz de adyacencia para un grafo

"La matriz de adyacencia es una matriz cuadrada que se utiliza como una forma de representar relaciones binarias."; aunque para nuestro caso será una de las formas de representar un grafo.

¿Por que matriz cuadrada? (si fuera profesor lo preguntaría para pescar a más de un distraído), la razón es que tanto las filas como las columnas representan cada uno de los nodos del grafo, si el grafo es de n nodos, la matriz correspondiente sería de n * n, es decir matriz cuadrada, fácil.

Continuemos analizando el paso de grafo a una matriz.

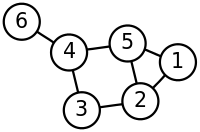
Como ya sabemos al tener 6 nodos nuestro grafo, nuestra matriz tendrá unas dimensiones de 6 * 6, es decir 6 filas y seis columnas.

Si nos fijamos en lo que consideraremos nuestro primer nodo, el nodo uno solo esta conectado con el nodo 2 y 5; en la fila 1 que representa el nodo 1 se ha marcado con ceros los nodos con que no se tiene relación y se ha fijado un 1 en los que si, el nodo 2 y 5.

Si nos fijamos en lo que consideraremos nuestro segundo nodo, el nodo dos esta conectado con el nodo 1, 3 y 5; en la fila 2 que representa el nodo 2 se ha marcado con ceros los nodos con que no se tiene relación y se ha fijado un 1 en los que si, el nodo 1, 3 y 5.

Análogamente hacemos de igual forma con los demás nodos hasta terminar el grafo.

Les dejo algunos ejemplo y un ejecutable en Java de mi autoría para que se diviertan.

Clic aquí para descargar ejecutable.

Métodos de ordenamiento usando java

Cuando tenemos una estructura de datos una de las operaciones más relevantes es ordenar el contenido de la misma, ya sea para hacerla más amistosa de leer o mejor aún para aplicar más operaciones sobre dichos datos como por ejemplo hacer búsquedas en ellas, (véase búsqueda binaria y búsqueda secuencial).

El ordenamiento en una estructura de datos la podemos definir como los posibles cambios aplicados a la posición de los datos que la llevaría a estar una relación de orden, ésta relación de orden puede ser alfabética, numérica, entre otras.




Aunque la formulación del problema es fácil y hasta cotidiana, tanto como dar una secuencia de números aleatorios a alguien y pedirle de los ordene de mayor a menor; existen muchos métodos para la resolución de éste problema, y aún en la actualidad se sigue trabajando en ello para lograr cada vez más rapidez y eficacia.

En éste blog abordaré varios de los métodos más usados para la ordenación de datos y que a su vez nos servirán como introducción a éste tema usando Java como lenguaje de programación.

Clic para ver el método de selección.
Clic para ver el método de inserción. (próximamente)
Clic para ver el método de burbuja. (próximamente)
Clic para ver el método de shell. (próximamente)

Método de ordenamiento por selección usando Java

Es un método poco eficiente pero fácil de entender, en caso de ordenar números éste consistirá en determinar cual es el menor de todos y ubicarlo en la primera posición, luego determinar cual es el segundo menor y ubicarlo en la segunda posición hasta terminar con todo los numero.

La cantidad de comparaciones para éste método de ordenamiento está dada por la fórmula: c(n) = (n² – n)/2; es decir para un arreglo de 10 elementos el numero de comparaciones es de (10² – 10)/2 = 45; en el siguiente código fuente al descomentariar la linea 7 y compilar notarán el número de comparaciones.

Analizando podemos darnos cuenta que aunque nuestro arreglo a mitad del proceso este ordenado, el método seguirá haciendo comparaciones innecesarios haciéndolo poco eficiente sobre todo para grandes cantidades de elementos.

Sin más preámbulos, el código:

class seleccion{
 public static void ordenar(int[] arreglo){
  int contador = 1;//solo util para contar las comparaciones
  for (int i = 0; i < arreglo.length - 1; i++){
   int min = i;
   for (int j = i + 1; j < arreglo.length; j++){
   //System.out.println("Comparacion #" + contador);
    contador++;
    if (arreglo[j] < arreglo[min]){
     min = j;
    }
   }
   if (i != min){
    int aux= arreglo[i];
    arreglo[i] = arreglo[min];
    arreglo[min] = aux;
   }
  }
 }
 public static void imprimirLista(int[] arreglo){
  for(int i = 0; i < arreglo.length;i++){
   System.out.print(arreglo[i]+",");
  }
  System.out.println();
 }
 public static void main(String[] args){
  int lista[] = {9,1,4,2,8,3,5,6,7,0};
  System.out.print("Lista desordenada: ");
  imprimirLista(lista);
  
  ordenar(lista);

  System.out.print("Lista ordenada: ");
  imprimirLista(lista);
 }
}

Deseaba en ésta entrada hacer una prueba de escritorio al método, pero haré algo mejor, agregaré comentarios de salida al codigo para detallar cada comparación de la lista que ustedes introduzcan, abajo está el link de descarga, espero les guste y hagan sus comentarios.

Descarga aqui codigo con prueba de escritorio

Recursividad usando java

Saludos lectores, aunque éste tema está muy bien documentado en Internet, a continuación lo expongo de manera fácil y como de costumbre con código.

Definición: Un algoritmo recursivo es un algoritmo que expresa la solución de un problema en términos de una llamada a sí mismo. La llamada a sí mismo se conoce como llamada recursiva o recurrente (Por Wikipedia).

En pocas palabras, usamos recursividad cuando un método se llama a sí mismo para resolver un problema.

Expongo un método no muy común para darlo como ejemplo, pero fácil de entender:

public class recursividad{
 private static int suma(int a,int b){
  return a + b;
 }
 private static int suma(int a,int b,int c){
  return suma(suma(a,b),c);
 }
 private static int suma(int a,int b,int c,int d){
  return suma(suma(a,b),suma(c,d));
 }
 private static int suma(int a,int b,int c,int d, int e){
  return suma(suma(a,b,c,d),e);
 }
 public static void main(String []args){
  int a = 1;
  int b = 3;
  int c = 4;
  int d = 5;
  int e = 6;
  System.out.println(suma(a,b));
  System.out.println(suma(a,b,c));
  System.out.println(suma(a,b,c,d));
  System.out.println(suma(a,b,c,d,e));
 }
}

El anterior código desde el punto de vista de algoritmo no es exactamente recursividad ya que éste codigo funciona gracias a una propiedad presente en Java llamada poliformismo; pero es un buen ejemplo de inicio para entender.

Si observamos el primer método suma que recibe por parámetros dos número enteros es el que hace la operación arismetica de la suma, los demás métodos suma se benefician de manera recursiva del primero.

Muchos problemas mátematicos se pueden resolver de manera recursiva, pero por lo general es el problema y nuestra forma de abordarlos lo que define si se puede o no resolver de manera recursiva.

Pasemos a un ejemplo más practico y usado para enseñar recursividad, hallar el factorial de un numero usando la recursividad en Java.

El factorial de un numero se define de la siguiente forma:

n! = 1 X 2 X 3 X 4 X ... X (n -1) X n

O de ésta otra forma más facil para nosotros: n! = 1 * 2 * 3 * 4 * ... * (n -1) * n

Para entender mejor miremos ejemplos y lo facil que es calculemos 5! que se lee factorial de 5.

5! = 1 * 2 * 3 * 4 * 5 =  120

Calculemos otros factoriales.

3! = 1 * 2 * 3 = 6

2! = 1 * 2 = 2

Surge una pregunta, cual es el factorial 0?, por definición el factorial de cero es uno, es decir ( 0! = 1 ), ¿Por que?, soy sincero, ésta respuesta la saben los matematicos y ellos la pueden explicar mejor que yo, con todo y demostración.

Antes de seguir hay algo muy importante al momento de hacer métodos recursivos, hay que tener un caso base; el caso base es el punto en el código donde acaba la recursividad, sin este caso base se generaría una recursividad infinita, más adelante mostraremos con ejemplo el caso base.

Sigamos calculando factoriales:

Ya sabemos que factorial de 5 es  1 * 2 * 3 * 4 * 5; pero podemos decir que es igual a (1 * 2 * 3 * 4) * 5; hasta aqui lo unico que hicimos fue agrupar (1 * 2 * 3 * 4) y multiplicarlo por 5; asi:

5! = 1 * 2 * 3 * 4 * 5 = (1 * 2 * 3 * 4) * 5 = 120

pero a que es igual  (1 * 2 * 3 * 4) ?

(1 * 2 * 3 * 4) = 4!

Es decir que:

5! = 4! * 5

Si se fijan aqui ya hay recursividad, para hallar el factorial de 5 necesitamos hallar el factorial de 4.

Este orden de idea resolveremos el factorial de 5 paso a paso, y usando algo asi como una prueba de escritorio.

Factorial de 5?
5! = ?

Factorial de 5 es factorial de 4 por 5
5! = 4! * 5

Pero no se cual es el factorial de 4, facil, factorial de 4 es factorial de 3 por 4
4! = 3! * 4

Pero no se cual es el factorial de 3, facil, factorial de 3 es factorial de 2 por 3
3! = 2! * 3

Pero no se cual es el factorial de 2, facil, factorial de 2 es factorial de 1 por 2
2! = 1! * 2

Pero no se cual es el factorial de 1, facil, factorial de 1 es factorial de 0 por1
1! = 0! * 1

Pero yo si se cual es el factorial de 0, por definición 0! = 1; éste es nuestro caso base.

Ahora toca devolverse para ir resolviendo lo calculos que dejamos pendientes atras asi:

si: 0! = 1

y si: 1! = 0! * 1

entonces:

1! = 1 * 1 = 1

si: 1! = 1

y si: 2! = 1! * 2
entonces:

2¡ = 1 * 2 = 2

si: 2! = 2

y si: 3! = 2! * 3
entonces:

3¡ = 2 * 3 = 6

si: 3! = 6

y si: 4! = 3! * 4
entonces:

4¡ = 6 * 4 = 24

si: 4! = 24

y si: 5! = 4! * 5
entonces:

5¡ = 24 * 5 = 120

Cuando nos regresamos a resolver las operaciones que dejamos pendientes, nuestros computadores también lo hacen cuando resuelven algoritmos recursivos, dichas operaciones pendientes por resolver las almacenan en las llamadas pilas de procesos, es por esta razón que nuestros algoritmos recursivos exigen más de nuestros computadores que los algoritmos no recursivos.

Una cosa curiosa que ustedes han notado, es que hacer nuestras pruebas de escritorio de algoritmos recursivos resultan largos pero ironicamente las linea de código que usamos es menor vs no recursivos.

Como ya habiamos visto la forma de representar el factorial de un numero es:

n! = 1 * 2 * 3 * 4 * ... * (n -1) * n; ésta es la forma iterativa y se resumen en una sucesión de multiplicaciones que parten de uno y terminan hasta el numero que deseamos calcular.

Clic aqui para ver el codigo para hallar factorial iterativamente.

Ahora miremos como representar el calculo de un número factorial usando recursividad:

n¡ = (n - 1)! * n

pero para tener encuenta el caso base para que no se nos valla la recursividad al infinito la definiremos mejor así:

Sin más preambulo, les comparto el sencillo código para calcular factorial de un número de manera recursiva.

public class factorial{
 private static double factorial(int n){
   if (n==0){//caso base
   return 1;
  }else{
   return (factorial(n-1))*n;
  }
 }
 public static void main(String []args){
  System.out.print(factorial(5));
 }
}

Otro problema que se puede resolver recursivamente es la sucesión de Fibonacci, el codigo ya lo hice en una entrada anterior, aquí te dejo el link

Chao y exitos a todos

DJ Java Decompiler

Saludos a todos, me gustaría compartir con ustedes esta útil herramienta DJ Java Decompiler, que nos permite descompilar archivos de java class-file y guardarlos posteriormente en archivos de textos de manera simple y fácil.

Es compatible para las plataformas Windows 7, Windows 8, Windows NT/2000, Windows NT/2000/2003/SBS2003, Windows Vista, Windows XP.

Funciona descompilando y/o reconstruyendo el código fuente original de los archivos CLASS binarios compilados.

Ademas esta aplicación no necesita tener instalado Java para funcionar y como punto adicionar sirve como editor y todas las funciones típicas.

DJ Java Decompiler es adecuado para el estudio de bytescode de Java. El programa permite a los usuarios guardar, imprimir, editar y compilar el código Java generado. Incluido Applet Tag Editor permite a los usuarios crear applets rápidamente.

Aquí les dejo el link para que descarguen una versión trial y exploren esta herramienta

Link de descarga trial

Si les gustó pueden tener la versión completa en este otro link, descarga completa

EXITOS

Web scraping para consultar contenido en paginas web ajenas, llenar formularios y capturar respuesta usando Java.

Saludos a todos.

La siguiente entrada resolverá las siguientes incógnitas:

• ¿Cómo capturar el contenido de una pagina web usando Java?
• ¿Cómo llenar con datos un formulario de una web ajena y enviar los datos usando Java?
• ¿Cómo llenar con datos un formulario de una web ajena, enviar los datos y capturar la respuesta usando Java?

La solución a las anteriores dudas nos será de mucha utilidad si por ejemplo tienes muchos datos que deseas consultar en un formulario web y deseas automatizar dicha tarea.

Empecé a practicar web scraping sin saber que lo hacia, a mi esposa le encomendaron la tarea de consultar un poco mas de 1000 cédulas (dni en otros países) para determinar, mesa de votación, lugar y dirección donde debía realizar el sufragio para elección de senado y cámara en mi país Colombia, todo esto lo debía hacer desde una desde la pagina que el gobierno habilita http://wsr.registraduria.gov.co/servicios/elec-presidente2014.htm.

Mi esposa me solicitó ayuda para realizar la descomunal tarea, para mi dicha tarea es tediosa y representa perder mi tiempo en algo que no quería hacer, pesé que debía haber una forma de automatizar dicha tarea; así que con ayuda de mi amigo Google nos pusimos en la tarea de averiguar como hacer tal cosas.

Las sugerencia que encontramos nos dirigirían a que debía integrar un web browser a una aplicación Java, después de intentar con muchas librerías de las cuales la mayoría hacían el problema más grande, me quede con htmlunit.

¿Porque integrar un web browser? Mi idea era emular un navegador web y consultar dato por dato, pero aclaro que esto no lo haría yo, lo haría mi PC el cual no se aburre y hace esta tarea mucho más rápido que yo.

Les dejo un vistazo de la aplicación funcionando.

Es hora de ver código,  le ofrezco uno muy básico y fácil de comprender que les ayudara a hacer cosas mas complicadas después; en el código emulé una consulta al buscador de Google.

package scraping;

import com.gargoylesoftware.htmlunit.FailingHttpStatusCodeException;
import com.gargoylesoftware.htmlunit.WebClient;
import com.gargoylesoftware.htmlunit.html.HtmlForm;
import com.gargoylesoftware.htmlunit.html.HtmlPage;
import com.gargoylesoftware.htmlunit.html.HtmlSubmitInput;
import com.gargoylesoftware.htmlunit.html.HtmlTextInput;
import java.io.IOException;
import java.util.logging.Level;
import java.util.logging.Logger;

/**
 *
 * @author rey salcedo
 */
public class Scraping {

    /**
     * @param args the command line arguments
     */
    public static void main(String[] args) {
        //emulamos un navegador web
        final WebClient webClient = new WebClient();

        try {
            //Pagina donde se hara la consulta
            HtmlPage page1 = webClient.getPage("https://www.google.com.co/search");
            
            //nombre del formulario
            final HtmlForm form = page1.getFormByName("f");
            //el valor "f" no es arbitrario es el nombre del formulario web de google
            
            //nombre de la caja de texto
            final HtmlTextInput textField = form.getInputByName("q");
            //el valor "q" no es arbitrario es el nombre de la caja de texto del formulario web de google

            //nombre del boton del formulario
            final HtmlSubmitInput button = form.getInputByName("btnG");
            //el valor "btnG" no es arbitrario es el nombre del boton del formulario web de google
                        
            //llenamos la caja de texto
            textField.setValueAttribute("usandojava");

            //Creamos la pagina que nos devolverá el resultado
            final HtmlPage pageResultado;
            
            //hacemos clic en el boton del formulario y asignamos el resultado a la pagina pageResultado
            pageResultado = button.click();
            
            //imprimimos el resultado
            System.out.println(pageResultado.asText());
            
            //cerramos el navegador emulado, para liberar todo esto de la memoria
            webClient.closeAllWindows();
        } catch (IOException ex) {
            Logger.getLogger(Scraping.class.getName()).log(Level.SEVERE, null, ex);
        } catch (FailingHttpStatusCodeException ex) {
            Logger.getLogger(Scraping.class.getName()).log(Level.SEVERE, null, ex);
        }
    }
}

Advierto que para el caso del formulario de google no es estrictamente necesario llenar un formulario como lo he hecho, ya que solo bastas con un simple link https://www.google.com.co/search?q=usandojava

Para la consulta de los nombre de los componentes les sugiero que descarguen la pagina web donde está el formulario y como nota importante les sugiero de no usen chrome, mejor usen FireFox ya que chrome no me daba los nombres apropiados de los componentes del formulario, para la descarga de las librerías necesarias les dejo el link de la pagina oficial http://sourceforge.net/projects/htmlunit/files/htmlunit/

Como siempre esperando serles de ayuda.

No olviden comentar.