Construya su propia computadora (implementacion de Simpletron).

Abajo Link para descargar código fuente.

Este es el titulo de un ejercicio que ví propuesto en el libro "Como programar en Java, 5ta edicion pagina 294" y que nos lleva a la implementacion de un sistema llamado Simpletron para la ejecucion de ordenes estilo ensamblador, la implemetacion es bastante basica, pero me gusta mucho y quiero aqui compartir con ustedes.

Aqui esta el link para que lean las especificaciones que aparecen en ellibro.

Les resumo que, el programa esta dotado de una memoria que almacena maximo 100 numeros enteros (en el libro llamados palabras), ademas de una variable llamada acumulador de tipo entero; en la memoria almacenamos ordenenes compuestas por un numero de 4 digitos (palabras) donde los dos primeros representan un codigo de operacion y los dos numeros restantes operando, ejemplo 1011 asi:

|10|11|
 |  |
 |  +--- operando
 +--- Codigo de operacion

Claro que el ejercicio propuesto no termina alli, pues en los ejercicios 20.26 y 20.27 del mismo libro proponen crear con este un compilador para un lenguaje de alto nivel; en la medida de lo posible estare gastandole algo de tiempo al ejercicio.

Al final expongo la implementacion que hice para ustedes, aunque no lo hice a cabalidad como el libro lo pide, empezando en que no use aplet para escribir un codigo mas simple.


 
Los codigo de operacion son los siguiente (Sugeridos en el libro)

Operaciones de entrada/salida:
10:Lee una palabra desde el teclado y la introduce en una ubicación específica dememoria.
11:Escribe una palabra de una ubicación específica de memoria y la imprime en lapantalla.


Operaciones de carga/almacenamiento:
20:Carga una palabra de una ubicación específica de memoria y la coloca en elacumulador.
21:Almacena una palabra del acumulador dentro de una ubicación específica dememoria.


Operaciones aritméticas:
30:Suma una palabra de una ubicación específica de memoria a la palabra en elacumulador (deja el resultado en el acumulador).:
31:Resta una palabra de una ubicación específica de memoria a la palabra en elacumulador (deja el resultado en el acumulador).:
32:Divide una palabra de una ubicación específica de memoria entre la palabra enel acumulador (deja el resultado en el acumulador).
33:Multiplica una palabra de una ubicación específica de memoria por la palabra enel acumulador (deja el resultado en el acumulador).


Operaciones de transferencia de control:
40:Bifurca hacia una ubicación específica de memoria.
41:Bifurca hacia una ubicación específica de memoria si el acumulador es negativo.
42:Bifurca hacia una ubicación específica de memoria si el acumulador es cero.
43:Alto. El programa completó su tarea.





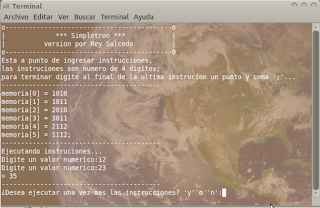
Pasos para pedir dos numero enteros, sumarlos y mostrar el resultado;
1010 (Pedir un numero y guardarlo en memoria en la posicion 10)
1011 (Pedir un numero y guardarlo en memoria en la posicion 11)
2010 (Cargar lo que este en la posicion 10 de la memoria al acumulador)
3011 (Sumar lo que este en la posicion 11 y el acumulador, el resultado se guardara en el acumulador)
2112 (Almacenar lo que este en el acumulador a la memoria en la posicion 12)
1112; (Imprimir lo que este en la memoria en la posicion 12)

Nota: ver que la ultima instrucion termina en punto y coma ';'

Pantallazo de la aplicación:


--------------------------------------------------------------------------------------------------
Hallar el mayor de tres numeros;
1020
1021
1022
2020
3121
4109
2020
2123
4011
2021
2123
3122
4115
1123
4300
1122;

Nota: ver que la ultima instrucion termina en punto y coma ';'

Codigo fuente clic aqui.



Comenta acerca del código.

Teoria de grafos. Imprementacion de un grafo, recorrido en profundidad y anchura.

(Al final de la pagina codigo para descargar).

También te puede interesar "Implementacion en Java del Algoritmo de Dijkstra", "Aplicacion de mapas, usando grafos y Dijkstra"

Definicion de grafos: Un grafo es un conjunto, no vacío, de objetos llamados vértices (o nodos) y una selección de pares de vértices, llamados aristas (edges en inglés) que pueden ser orientados o no. Típicamente, un grafo se representa mediante una serie de puntos (los vértices) conectados por líneas (las aristas). (Por Wikipedia).

-----------------------------------------------------------------------------
Existen muchas forma de representar grafos, la mas comun es usar circulos para los nodos y lineas para las aristas.
La que use para modelar y luego implemetar el grafo consiste en un arreglo de nodos, los cuales pueden apuntar a otros nodos dentro del mismo arreglo asi:


Podemos interpretarlo de la siguiente forma:
[A] tiene como adyancentes a [B],[C],[F]
[B] tiene como adyancentes a [A],[F]
[C] tiene como adyancentes a [A],[D]
[D] tiene como adyancentes a [C]
[F] tiene como adyancentes a [A],[B]
-----------------------------------------------------------------------------

Recorrido o búsqueda en profundidad (en inglés DFS o Depth First Search): es un algoritmo que permite recorrer todos los nodos de un grafo o árbol (teoría de grafos) de manera ordenada, pero no uniforme. Su funcionamiento consiste en ir expandiendo todos y cada uno de los nodos que va localizando, de forma recurrente, en un camino concreto. Cuando ya no quedan más nodos que visitar en dicho camino, regresa (Backtracking), de modo que repite el mismo proceso con cada uno de los hermanos del nodo ya procesado.(Por Wikipedia).

Búsqueda en anchura (en inglés BFS - Breadth First Search): es un algoritmo para recorrer o buscar elementos en un grafo (usado frecuentemente sobre árboles). Intuitivamente, se comienza en la raíz (eligiendo algún nodo como elemento raíz en el caso de un grafo) y se exploran todos los vecinos de este nodo. A continuación para cada uno de los vecinos se exploran sus respectivos vecinos adyacentes, y así hasta que se recorra todo el árbol.(Por Wikipedia).

------------------------------------------------------------------------------------------
Algorito de profundiad por Wikipedia

DFS_Visitar(nodo u)
 estado[u] ← VISITADO
 tiempo ← tiempo + 1
 d[u] ← tiempo
 PARA CADA v ∈ Vecinos[u] HACER
 SI estado[v] = NO_VISITADO ENTONCES
 padre[v] ← u
 DFS_Visitar(v)
 estado[u] ← TERMINADO
 tiempo ← tiempo + 1
 f[u] ← tiempo

Algorito de anchura por Wikipedia

 BFS(grafo G, nodo_fuente s)
{
// recorremos todos los vértices del grafo inicializándolos a NO_VISITADO,
// distancia INFINITA y padre de cada nodo NULL
for u ∈ V[G] do
{
estado[u] = NO_VISITADO;
distancia[u] = INFINITO; /* distancia infinita si el nodo no es alcanzable */
padre[u] = NULL;
}
estado[s] = VISITADO;
distancia[s] = 0;
Encolar(Q, s);
while !vacia(Q) do
{
// extraemos el nodo u de la cola Q y exploramos todos sus nodos adyacentes
u = extraer(Q);
for v ∈ adyacencia[u] do
{
if estado[v] == NO_VISITADO then
{
estado[v] = VISITADO;
distancia[v] = distancia[u] + 1;
padre[v] = u;
Encolar(Q, v);
}
}
}
}

Particularmente puedo comentarles que el recorrido en profundidad consiste en:

1: Tener un nodo inicio.
2: Adjuntarlo a la pila.
3: Verificar si la pila esta vacia, mientras no este vacia...
4: Tomo un nodo de la pila (en el caso de la pila el ultimo que se ingresó) y lo marco como visitado.
5: Proceso el nodo que tome del paso 4 (El proceso puede ser por ej: imprimirlo).
6: Adjunto a la pila los nodos adyacente del nodo tomado en el paso 4.
7: Regreso al paso 3, hasta que la pila este vacia.

Asi implemente el metodo.

Algorito de profundiad por Rey Salcedo

public void recorrerProfundidadI(Nodo nodoInicio){
        if(nodoInicio != null){
            pila.addNodo(nodoInicio);
            while(pila.size() > 0){
                Nodo nodoVisitado = pila.getNodo();
                if(nodoVisitado.visitado == false){
                    nodoVisitado.visitado = true;
                    System.out.print(nodoVisitado.getDato()+",");                
                    llenarPilaNodosAdyacentes(nodoVisitado);
                }
            }
        }
    }

Para el caso del recorrido en anchura, es analogo, solo tienes que remplazar la pila por una cola (tener en cuenta que en la cola el primero en entrar es el primero en salir).

Tomemos el grafo del dibujo como ejemplo:

Lo contruimos de la siguiente forma:
----------------------------------------------

public static void llenandoGrafo(){
 grafo = new Grafo();
 
 // creamos los nodos del grafo.
 grafo.adjuntarNodo(new Nodo("A"));
 grafo.adjuntarNodo(new Nodo("B"));      
 grafo.adjuntarNodo(new Nodo("C"));
 grafo.adjuntarNodo(new Nodo("D"));
 grafo.adjuntarNodo(new Nodo("F"));
       
 grafo.crearEnlaces("A","B");// de A hacia B
 grafo.crearEnlaces("B","A");// de B hacia A
 /*
  * Lo anterior lo hacemos por ser un grafo no dirigido...
  * En caso de ser un grafo con peso esto no estaria muy bien que digamos
 */
     
 grafo.crearEnlaces("A","C");
 grafo.crearEnlaces("C","A");
        
 grafo.crearEnlaces("A","F");
 grafo.crearEnlaces("F","A");
        
//grafo.crearEnlaces("B","A");//Esta enlace ya existe
//grafo.crearEnlaces("A","B");//Esta enlace ya existe
        
 grafo.crearEnlaces("B","F");
 grafo.crearEnlaces("F","B");
        
//grafo.crearEnlaces("C","A");//Esta enlace ya existe
//grafo.crearEnlaces("A","C");//Esta enlace ya existe
        
 grafo.crearEnlaces("C","D");
 grafo.crearEnlaces("D","C");
        
//grafo.crearEnlaces("D","C");//Esta enlace ya existe
//grafo.crearEnlaces("C","D");//Esta enlace ya existe
        
//grafo.crearEnlaces("F","A");//Esta enlace ya existe
//grafo.crearEnlaces("A","F");//Esta enlace ya existe
        
//grafo.crearEnlaces("F","B");//Esta enlace ya existe
//grafo.crearEnlaces("B","F");//Esta enlace ya existe

}

----------------------------------------------




Bueno y ya para terminar, corremos los algoritmo de Recorrido que nos arroga la siguiente salida:

----------------------------------------------
Recorrido en profundidad
[A]A,
[B]
[BC]
[BCF]F,C,
[BD]D,B,
----------------------------------------------
Recorrido en Amplitud
[A]A,
[B]
[BC]
[BCF]B,C,
[FD]F,D,
----------------------------------------------
Donde lo que esta en conchete es el contenido en la pila, y lo que esta afuera es lo que sale de la pila.
Para descargar codigo fuente, clic aqui.


También te puede interesar "Implementacion en Java del Algoritmo de Dijkstra"



Comenta acerca del código.