Saludos a todos.
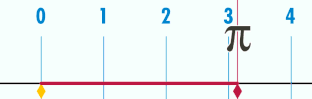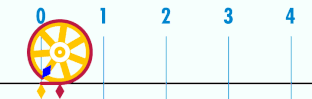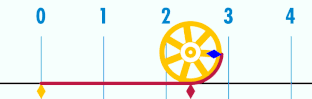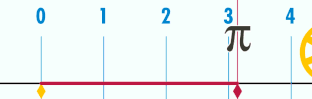
Hace muchísimo tiempo cuando curioseaba el lenguaje Pascal y antes de dormir me puse a pesar en la geometría del circulo y recordé las clases de colegio donde me decían que el valor de pi no era mas que la longitud de la circunferencia dividida entre su diámetro.
Tenia presente que midiendo la circunferencia y el diámetro de un plato redondo por ejemplo solo hallaría un valor aproximado de pi, y que dicho valor más exacto sólo lo podían hacer los matemáticos y sus demostraciones, cosa que difícilmente lograría yo.
Siempre he sido regular en matemáticas, para algunos muy bueno, la verdad no lo creo; pero sí me consideraba mejor en la geometría y dibujo técnico.
De tanto pensar en círculos, matemática y geometría llego a mi una forma de hallar el valor de pi sin hacer demostraciones, gracias a que recordé que había leído en alguna parte la teoría que mas o menos dice "Un circulo es una figura geométrica con muchos lados que equidistan de un centro o eje"
Se me prendió el bombillo, me dije, tomare un cuadrado del cual conozco su diámetro y le agregare más lados calculado de los ya existentes sin cambiar el diámetro del mismo, es decir que el diámetro sera una constante; la suma de sus lados me darían el perímetro el cual dividiría por el diámetro y me daría el valor aproximado de pi, si hago esto muchas veces me acercaré cada vez más a pi; en otras palabras le agregare más lados al cuadrado tratando de convertirlo en un circulo.
Tome lápiz, cuaderno y comencé ha calcular, para el caso de un cuadrado de diámetro 1 los lados medirían 0,707106781, ya que según Pitágoras:
h^2 = co^2 + ca^2
Como para un cuadrado sus lados son igual, es decir sus catetos, nos quedaría:
h^2 = co^2 + co^2
h^2 = 2 * co^2
Sacamos raíces a ambos términos de cada igualdad
h = √2 * co
finalmente
co = h/√2
siendo la hipotenusa nuestro diámetro y remplazando...
co = 1/√2 = 0,707106781;
Listo ya tengo los datos de mi cuadrado, como los cuadrados tienen 4 lados el perímetro sería (0,707106781 * 4) = 2,828427125
Nuestro primer valor aproximado para pi seria:
2,828427125/1 = 2,828427125
2,828427125 es un valor muy distante al verdadero valor de pi; lo que sigue ahora es usando geometría agregarle más lados a figura y calcularlos sin cambiar el diámetro (1) y recalcular el valor de pi; en la practica debía recalcular miles de veces para llegar a un valor decente de pi.

Tome nuevamente mi cuaderno y lápiz, y escribir un programa en Pasca (en esa época no tenia computador, así que me tocaba a papel y compilar en mi cabeza) para luego esperar el sábado que tenia nuevamente contacto con un computador; para sorpresa mía el día que pase mi programa a computador funciono sin problemas dándome el valor de pi tal cual una calculadora, estaba muy excitado al llegar muy cerca al valor de pi sin ser matemático.
Como mencione al inicio, eso paso hace mucho tiempo; y hoy que empece a recordar me ha sido duro reconstruir el programa, sospecho que es por mi pereza de hacer algo dos veces, así que investigue algo que me ayudara a recordar y me tope conque ya eso lo habían hecho Arquimedes y lo llamó Método exhaustivo, aunque mi método es ligeramente distinto, así que más pereza me da reconstruirlo, pero en un futuro lo haré para ustedes.
Pero como es costumbre escribir código en cada una de mis entradas, me tope con la Fórmula de Leibniz que no es más que una sumatoria que tiende al infinito y que es fácil programar.
//Autor Rey Salcedo
class FormulaLeibniz{
public static double formula(int repeticiones){
double pi = 0;
for(int n = 0;n < repeticiones;n++){
pi += ((Math.pow(-1,n))/(2*n + 1));
}
return pi*4;
}
public static void main(String[] args){
System.out.println(formula(100000000));
}
}
Espero le sirva y les sea de agrado