Al programar, muchas veces nos vemos en la necesidad de validar si ciertas cadenas de textos cumplen o no con un patrón especifico, por ejemplo, saber si un texto esta compuesto en su totalidad por números, generalmente lo resolvemos de la siguiente forma:
O tal vez así:
En otros casos necesitamos buscar fragmentos de textos en cadenas muchos más largas, por ejemplo, si estamos construyendo un editor de texto en java lo podemos hacer así:
Admito que el código anterior pudo haber salido mas corto.
Para finalizar, muchas veces nos topamos con la necesitad de extraer textos o quizás remplazarlo de una cadenas más larga, estos dos últimos casos seria lo mismo, extraer un texto es equivalente a remplazarlo por una cadena vacía ("").
Los métodos que anteriormente escribí puede que sean de mucha utilidad, pero hay una técnica que nos facilita la resoluciones de problemas de este tipo y además nos agrega robustez a nuestros programas, dicha técnica hace uso de algo llamado Expresiones Regulares.

EXPRESIONES REGULARES
En el área de la programación las expresiones regulares son un método por medio del cual se pueden realizar búsquedas dentro de cadenas de caracteres. Sin importar si la búsqueda requerida es de dos caracteres en una cadena de 10 o si es necesario encontrar todas las apariciones de un patrón definido de caracteres en un archivo de millones de caracteres, las expresiones regulares proporcionan una solución para el problema. Adicionalmente, un uso derivado de la búsqueda de patrones es la validación de un formato específico en una cadena de caracteres dada, como por ejemplo fechas o identificadores. Por Wikipedia
El uso de expresiones regulares no es nada difícil, basta con decir que en muchas ocasiones hacemos uso de ellas sin darnos cuenta, por ejemplo, si queremos referirnos a cualquier archivo de extensión jpg solemos expresarlo asi "*.jpg", si queremos buscar archivos de textos que empiecen con la letra "a" lo hacemos con la expresión "a*.txt"; lo anterior es una de las forma en que hacemos uso de las expresiones regulares en la informática, aunque poco a poco y según nuestras necesidades estas se harán más complejas, pero con práctica y dedicación lograremos comprenderlo y aplicarlo en nuestros proyectos.
Antes de empezar con ejemplos de expresiones regulares usando Java, sugiero descargar la aplicación kiki las cual esta disponible tanto para Windows como para Gnu/Linux, en mi caso particular solo hay que usar el Centro de software de Ubuntu y listo.
public boolean esNumero(String cadena){
try {
Integer.parseInt(cadena);
return true;
} catch (Exception e) {
return false;
}
}
O tal vez así:
public boolean esNumero(String cadena){
char numeros[] = {'1','2','3','4','5','6','7','8','9','0'};
boolean bandera = true;
for(char charCadena:cadena.toCharArray()){
boolean banderaTemp = false;
for(char charNumero:numeros){
if(charCadena != charNumero){
banderaTemp |= false;
}else{
banderaTemp |= true;
}
}
bandera &= banderaTemp;
}
return bandera;
}
En otros casos necesitamos buscar fragmentos de textos en cadenas muchos más largas, por ejemplo, si estamos construyendo un editor de texto en java lo podemos hacer así:
public int buscarPosicionInicio(String cadenaABuscar,String cadenaDondeBuscar){
int pos = cadenaDondeBuscar.indexOf(cadenaABuscar);
if(pos == -1){
System.out.println("El texto no fue encontrado");
}
return pos;
}
Admito que el código anterior pudo haber salido mas corto.
Para finalizar, muchas veces nos topamos con la necesitad de extraer textos o quizás remplazarlo de una cadenas más larga, estos dos últimos casos seria lo mismo, extraer un texto es equivalente a remplazarlo por una cadena vacía ("").
Los métodos que anteriormente escribí puede que sean de mucha utilidad, pero hay una técnica que nos facilita la resoluciones de problemas de este tipo y además nos agrega robustez a nuestros programas, dicha técnica hace uso de algo llamado Expresiones Regulares.

EXPRESIONES REGULARES
En el área de la programación las expresiones regulares son un método por medio del cual se pueden realizar búsquedas dentro de cadenas de caracteres. Sin importar si la búsqueda requerida es de dos caracteres en una cadena de 10 o si es necesario encontrar todas las apariciones de un patrón definido de caracteres en un archivo de millones de caracteres, las expresiones regulares proporcionan una solución para el problema. Adicionalmente, un uso derivado de la búsqueda de patrones es la validación de un formato específico en una cadena de caracteres dada, como por ejemplo fechas o identificadores. Por Wikipedia
El uso de expresiones regulares no es nada difícil, basta con decir que en muchas ocasiones hacemos uso de ellas sin darnos cuenta, por ejemplo, si queremos referirnos a cualquier archivo de extensión jpg solemos expresarlo asi "*.jpg", si queremos buscar archivos de textos que empiecen con la letra "a" lo hacemos con la expresión "a*.txt"; lo anterior es una de las forma en que hacemos uso de las expresiones regulares en la informática, aunque poco a poco y según nuestras necesidades estas se harán más complejas, pero con práctica y dedicación lograremos comprenderlo y aplicarlo en nuestros proyectos.
Antes de empezar con ejemplos de expresiones regulares usando Java, sugiero descargar la aplicación kiki las cual esta disponible tanto para Windows como para Gnu/Linux, en mi caso particular solo hay que usar el Centro de software de Ubuntu y listo.
 |
| Captura de Kiki en acción |
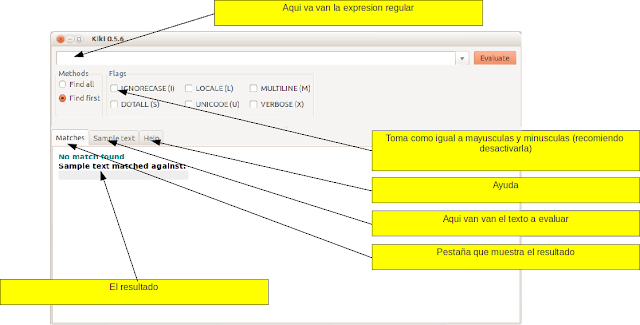 |
| Anotaciones para usar kiki |
Existen una seria de normas para construir de manera correcta nuestras expresiones regulares para java y estas las podemos ver recopiladas en la pagina oficial de Oracle http://docs.oracle.com/javase/7/docs/api/java/util/regex/Pattern.html, aunque están en ingles al traducirla se entiende muy bien; usaremos las más usadas que nos darán bases para posteriormente abarcar las demás.
| [abc] | Representa un carácter que puede ser 'a' ó 'b' ó 'c'. |
| [^abc] | Representa cualquier carácter excepto 'a' y 'b' y 'c'; en este caso cuando digo cualquier caracter, no me refiero solo a letras. |
| [a-z] | Representa el rango comprendido de la 'a' hasta la 'z', ojo no incluye 'ñ', vocales con tildes, ni consonantes con diéresis, en pocas palabras solo se aceptan el alfabeto ingles. |
| [a-zñ] | Representa el rango comprendido de la 'a' hasta la 'z', esta vez si incluye 'ñ', ojo solo incluye a la 'ñ', si queremos incluir más caracteres los colocamos al lado de la 'ñ'. |
| [A-Z] | Representa el rango comprendido de la 'A' hasta la 'Z', ojo no incluye 'ñ', solo el alfabeto ingles. |
| [a-zA-Z] | Representa el rango comprendido de la 'a' hasta la 'z' ó 'A' hasta la 'Z',pero solo el alfabeto ingles. |
| [a-d[m-p]] | Es equivalente a [a-dm-p], nótese que es parecido a la expresión anterior, representa el rango comprendido de la 'a' hasta la 'b' y 'm' hasta la 'p', es decir solo quedan incluidas 'a','b','c','d' y 'm','n','o','p'. |
| [a-z&&[def]] | Es equivalente a [def], es la intersección del conjunto de la 'a' hasta la 'z' y el conjunto 'd','e','f', el resultado es el mismo conjunto 'd','e','f'; aunque se ve innecesario esta expresión nos ayudara a comprender la que sigue. |
| [a-z&&[^def]] | Representa la intersección del conjunto de la 'a' hasta la 'z' y el conjunto todo el abecedario excepto los caracteres 'd','e','f', el resultado es el conjunto del abecedario excluyendo 'd','e','f'. |
| [a-z&&[^m-p]] | Representa la intersección del conjunto de la 'a' hasta la 'z' y el conjunto todo el abecedario excepto los caracteres 'm','n','o','p'. |
Nota: Todas la expresiones descritas anteriormente solo representan un carácter.
Ahora veamos dos caracteres más que nos ayudaran a representar expresiones más largas, '*' y el '+'; el primero representa "cero o más" mientras el segundo "uno o más"; hagamos algunos ejemplos usando java para que sea mas fácil de entender.
Usaremos el siguiente código para evaluar nuestros ejercicios, y en la practica veremos lo útil que será usar expresiones regulares.
import java.util.regex.Pattern;
public class Ejemplo {
public static void main(String[] args) {
String expresionRegular = "[abc]";
String cadenaAEvaluar = "a";
boolean b = Pattern.matches(expresionRegular,cadenaAEvaluar);
if(b){
System.out.println("La expresion SI representa la cadena a evaluar");
}else{
System.out.println("La expresion NO representa la cadena a evaluar");
}
}
}
Donde las variables expresionRegular y cadenaAEvaluar la modificaremos según el ejercicio.
Cuando:
expresionRegular = "[abc]";
cadenaAEvaluar = "a";
El resultado sera "La expresión SI representa la cadena a evaluar"
Sin embargo usamos otras letra distintas a 'a' ó 'b' ó 'c', ó mas de un carácter en cadenaAEvaluar, nos arrogara el resultado "La expresión NO representa la cadena a evaluar".
Cuando:
expresionRegular = "[0-1]";
cadenaAEvaluar = "a";
El resultado sera "La expresión NO representa la cadena a evaluar"
Para que la cadenaAEvaluar sea correcta, debemos introducir un numero, ejemplo "2"
Como ejercicio propongo que observemos los resultados con las demás expresiones.
Continuemos, ahora cabe la pregunta, ¿y si quiero evaluar mas de un carácter?
Recordemos el método isNumero propuesto al inicio, que nos dice si una cadena es un numero, usando expresiones regulares expresionRegular seria igual a "[0-9]+" que expresa una cadena 1 ó mas caracteres compuestos por números, el método quedaría más corto:
public boolean esNumero(String cadena){
return Pattern.matches("[0-9]+",cadena);
}
Otro ejemplo, digamos que deseamos saber si una cadena esta compuesta por un numero y una palabra en minúsculas, separada con un punto, ejemplo "12345.holamundo"
Para los números de uno o más cifras ya sabemos que es "[0-9]+", para las letras minúsculas es muy similar "[a-z]+", la expresión resultante quedara de la siguiente forma "[0-9]+.[a-z]+"
Es decir, cuando:
expresionRegular = "[0-9]+.[a-z]+"
cadenaAEvaluar = "12345.holamundo";
El resultado sera "La expresión SI representa la cadena a evaluar"
Ya puedes ver todo lo que puedes hacer?, puedes construir tu expresiones regulares para validar Email, números de celular del tipo "310-234-5678", direcciones web, etc
Aquí termino ésta primera parte, espero sus comentario para mejorar.
Y como siempre esperando serles de utilidad.

Hola buenas lo primero felicitarte por el blog. Yo quiero sacar de un array de cadenas una palabra y que me la cuantifique cuantas coincidencias hay en cada caso aquí dejo lo que tengo de código y el resultado que me da es para cada caso respectivamente 12100 y el resultado debería ser 12110
ResponderBorrarpackage jOnline;
import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
public class Juezes
{
public static void main(String[] args) {
Scanner teclado = new Scanner(System.in);
int casos = 0;
String[]frase2 = new String []
{
"Que me diga donde estan, le exijo!",
"Eres tan lento que te ganaria una oruga. Calla y salta, no le temas.",
"Esto es canela, verdad que si?",
"Stan Stan Lee Lee",
"Stan loo"
};
System.out.println("");
casos = teclado.nextInt();
System.out.println(frase2 [0]);
System.out.println(frase2 [1]);
System.out.println(frase2 [2]);
System.out.println(frase2 [3]);
System.out.println(frase2 [4]);
for (int i = 0; i<frase2.length;i++)
{
int contador = 0;
int x = 0;
String frase = frase2[i];
String palabra =
"[s].*[t].*[a].*[n].*[l].*[e]+";
palabra = palabra.toLowerCase();
Pattern patron = Pattern.compile(palabra.toLowerCase());
Matcher m1 = patron.matcher(frase2[i]);
while (m1.find(x))
{
x=m1.start()+1;
contador++;
}
System.out.println(contador);
}
}
}